TITLE: ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
AUTHOR: Xiangyu Zhang, Xinyu Zhou, Mengxiao Lin, Jian Sun
ASSOCIATION: Megvii Inc (Face++)
FROM: arXiv:1707.01083
CONTRIBUTIONS
- Two operations, pointwise group convolution and channel shuffle, are proposed to greatly reduce computation cost while maintaining accuracy.
MobileNet Architecture
In MobileNet and other works, efficient depthwise separable convolutions or group convolutions strike an excellent trade-off between representation capability and computational cost. However, both designs do not fully take the $ 1 \times 1 $ convolutions (also called pointwise convolutions in MobileNet) into account, which require considerable complexity.
Channel Shuffle for Group Convolutions
In order to address the mentioned issue, a straightforward solution is applying group convolutions on $ 1 \times 1 $ layers like what has been done on $ 3 \times 3 $ in MobileNet. However, if multiple group convolutions stack together, there is one side effect: outputs from a certain channel are only derived from a small fraction of input channels. This property blocks information flow between channel groups and weakens representation. To allow group convolution obtaining input data from different groups, for the feature map generated from the previous group layer, we can first divide the channels in each group into several subgroups, then feed each group in the next layer with different subgroups. It can be implemented by reshaping the previous output channel dimension into $ (g, n) $, transposing and then flattening it back as the input of next layer, which is called channel shuffle operation and illustrated in the following figure.

ShuffleNet Unit
The following figure shows the ShuffleNet Unit.
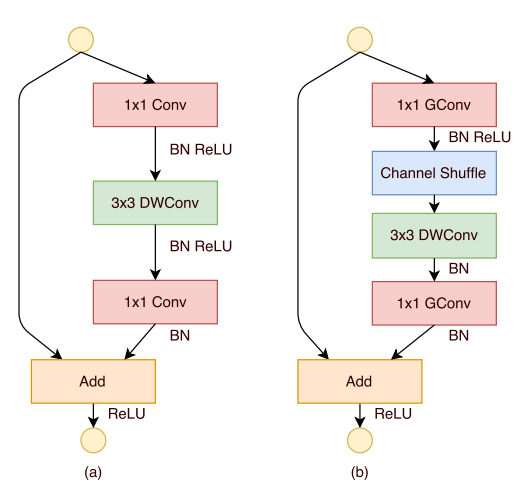
In the figure, (a) is the building block in ResNeXt, and (b) is the building block in ShuffleNet. Given the input size $ c \times h \times w $ and the bottleneck channels $ m $, ResNext has $ hw(2cm+9m^2/g) $ FLOPs, while ShuffleNet needs $ hw(2cm/g+9m) $ FLOPs.
Network Architecture
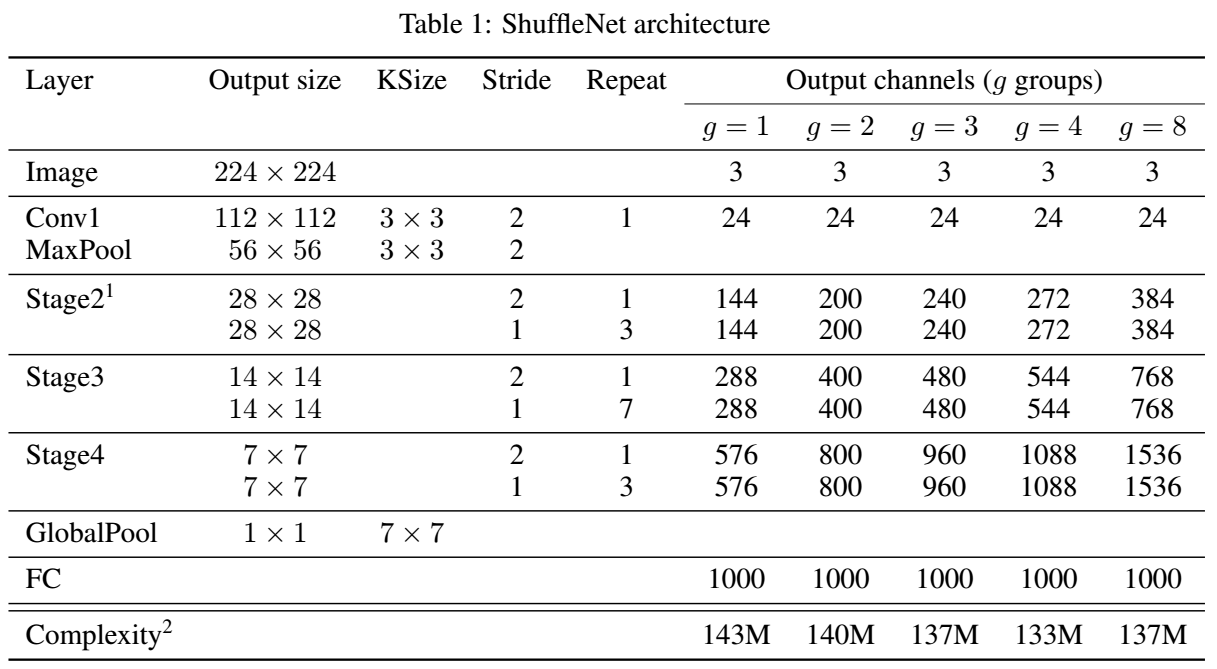
Comparison