Reading Note: ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression

TITLE: ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression

AUTHOR: Jian-Hao Luo, Jianxin Wu, Weiyao Lin

ASSOCIATION: Nanjing University, Shanghai Jiao Tong University

FROM: arXiv:1707.06342

CONTRIBUTIONS

1. A simple yet effective framework, namely ThiNet, is proposed to simultaneously accelerate and compress CNN models.
2. Filter pruning is formally established as an optimization problem, and statistics information computed from its next layer is used to prune filters.

METHOD

Framework

The framework of ThiNet compression procedure is illustrated in the following figure. The yellow dotted boxes are the weak channels and their corresponding filgers that would be pruned.

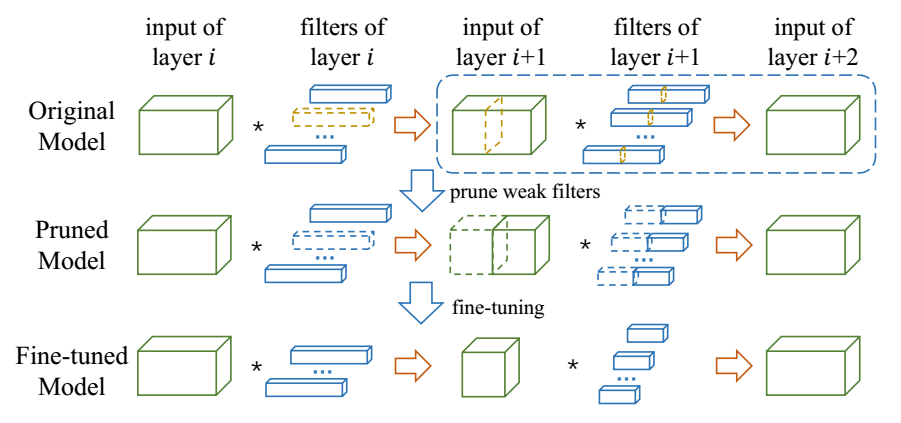
1. Filter selection. The output of layer $i + 1$ is used to guide the pruning in layer $i$. The key idea is: if a subset of channels in layer $(i + 1)$’s input can approximate the output in layer $i + 1$, the other channels can be safely removed from the input of layer $i + 1$. Note that one channel in layer $(i + 1)$’s input is produced by one filter in layer $i$, hence the corresponding filter in layer $i$ can be safely pruned.
2. Pruning. Weak channels in layer $(i + 1)$’s input and their corresponding filters in layer i would be pruned away, leading to a much smaller model. Note that, the pruned network has exactly the same structure but with fewer filters and channels.
3. Fine-tuning. Fine-tuning is a necessary step to recover the generalization ability damaged by filter pruning. For time-saving considerations, fine-tune one or two epochs after the pruning of one layer. In order to get an accurate model, more additional epochs would be carried out when all layers have been pruned.
4. Iterate to step 1 to prune the next layer.

Data-driven channel selection

Denote the convolution process in layer $i$ as A triplet

$$\left \langle \mathscr{I}_{i}, \mathscr{W}_{i}, \right \rangle$$

where $\mathscr{I}{i}$ is the input tensor, which has $C$ channels, $H$ rows and $W$ columns. And $\mathscr{W}{i}$ is a set of filters with $K \times K$ kernel size, which generates a new tensor with $D$ channels. Note that, if a filter in $\mathscr{W}{i}$ is removed, its corresponding channel in $\mathscr{I}{i+1}$ and $\mathscr{W}{i+1}$ would also be discarded. However, since the filter number in layer $i + 1$ has not been changed, the size of its output tensor, i.e., $\mathscr{I}{i+2}$, would be kept exactly the same. If we can remove several filters that has little influence on $\mathscr{I}_{i+2}$ (which is also the output of layer $i + 1$), it would have little influence on the overall performance too.

Collecting training examples

The training set is randomly sampled from the tensor $\mathscr{I}_{i+2}$ as illustrated in the following figure.

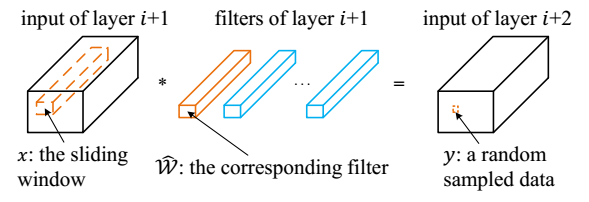
The convolution operation can be formalized in a simple way

$$\hat{y} = \sum_{c=1}^{C} \hat{x}_{c}$$

A greedy algorithm for channel selection

Given a set of $m$ training examples $\left{ (\mathrm{\hat{x}}{i}, \hat{y}{i}) \right}$, selecting channel can be seen as a optimization problem,

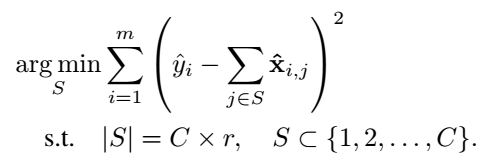
and it eauivalently can be the following alternative objective,

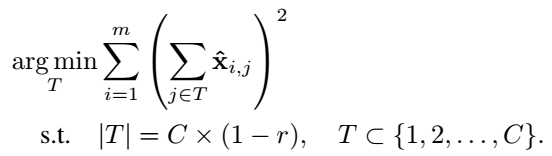
where $S \cup T = \left{ 1,2,…,C \right}$ and $S \cap T = \emptyset$. This problem can be sovled by greedy algorithm.

Minimize the reconstruction error

After the subset $T$ is obtained, a scaling factor for each filter weights is learned to minimize the reconstruction error.

Some Ideas

1. Maybe the finetue can help avoid the final step of minimizing the reconstruction error.
2. If we use this work on non-classification task, such as detection and segmentation, the performance remains to be checked.