TITLE: MobileNetV2: Inverted Residuals and Linear Bottlenecks
AUTHOR: Mark Sandler, Andrew Howard, Menglong Zhu, Andrey Zhmoginov, Liang-Chieh Chen
ASSOCIATION: Google
FROM: arXiv:1801.04381
CONTRIBUTION
- The main contribution is a novel layer module: the inverted residual with linear bottleneck.
METHOD
BUILDING BLOCKS
Depthwise Separable Convolutions. The basic idea is to replace a full convolutional operator with a factorized version that splits convolution into two separate layers. The first layer is called a depthwise convolution, it performs lightweight filtering by applying a single convolutional filter per input channel. The second layer is a $1 \times 1$ convolution, called a pointwise convolution, which is responsible for building new features through computing linear combinations of the input channels.
Linear Bottlenecks Consider. It has been long assumed that manifolds of interest in neural networks could be embedded in low-dimensional subspaces. Two properties are indicative of the requirement that the manifold of interest should lie in a low-dimensional subspace of the higher-dimensional activation space:
- If the manifold of interest remains non-zero vol-ume after ReLU transformation, it corresponds to a linear transformation.
- ReLU is capable of preserving complete information about the input manifold, but only if the input manifold lies in a low-dimensional subspace of the input space.
Assuming the manifold of interest is low-dimensional we can capture this by inserting linear bottleneck layers into the convolutional blocks.
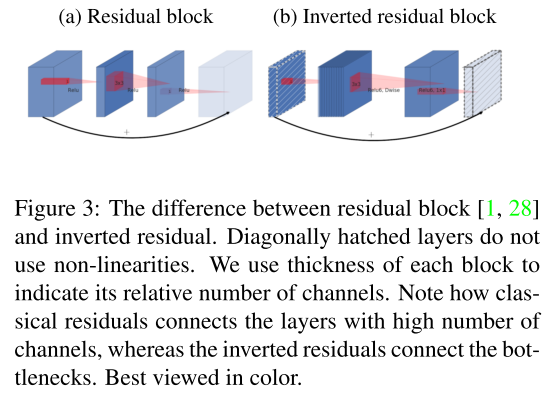
Inverted Residuals. Inspired by the intuition that the bottlenecks actually contain all the necessary information, while an expansion layer acts merely as an implementation detail that accompanies a non-linear transformation of the tensor, shortcuts are used directly between the bottlenecks. In residual networks the bottleneck layers are treated as low-dimensional supplements
to high-dimensional “information” tensors.
The following figure gives the Inverted resicual block. The diagonally hatched texture indicates layers that do not contain non-linearities. It provides a natural separation between the input/output domains of the building blocks (bottleneck layers), and the layer transformation – that is a non-linear function that converts input to the output. The former can be seen as the capacity of the network at each layer, whereas the latter as the expressiveness.
The framework of the work is illustrated in the following figure. The main idea of this work is to learn image aesthetic classification and vision-to-language generation using a multi-task framework.
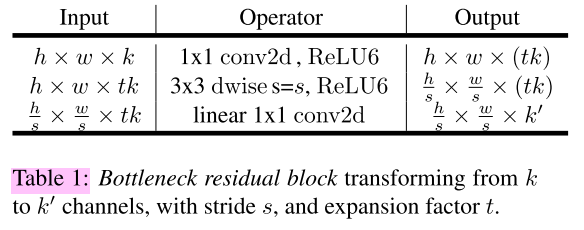
And the following table gives the basic implementation structure.
ARCHITECTURE

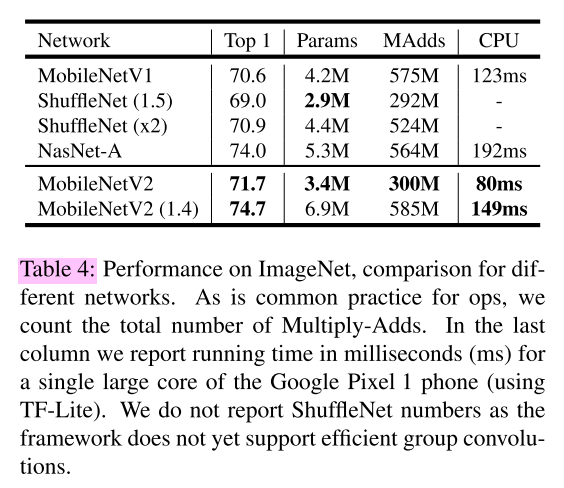
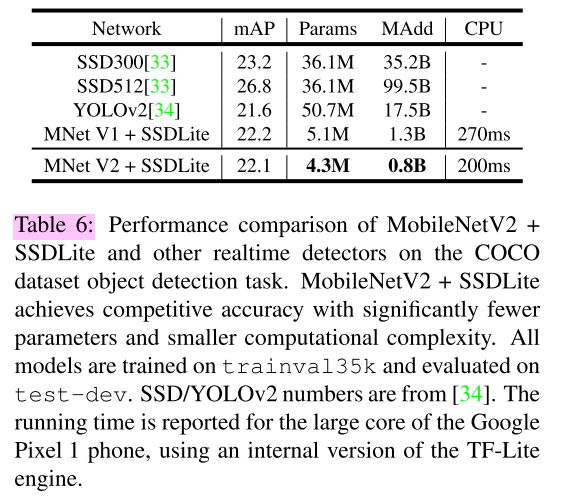
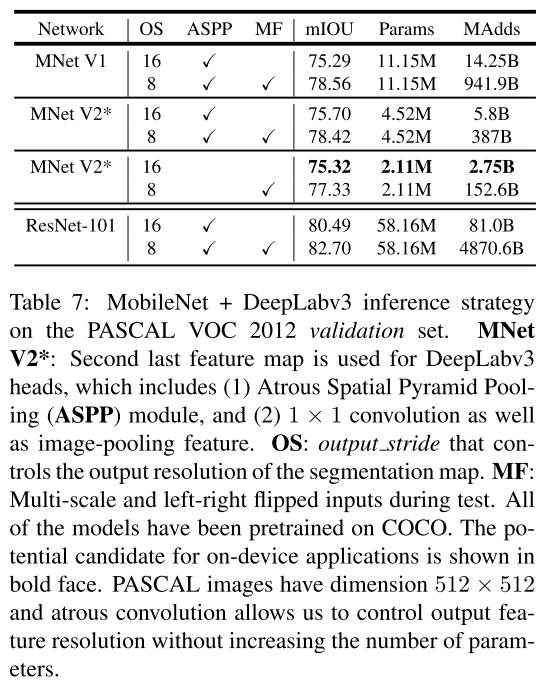
PERFORMANCE